Falando sobre Mínimo Múltiplo Comum

Uma das formas de despertar o interesse dos alunos nas aulas de matemática é aliar os conteúdos que estão sendo estudados a jogos ou atividades concretas. O jogo socializa, desenvolve a atenção, a concentração, a autoconfiança, promove a aprendizagem e torna a aula lúdica e interativa.

Neste post eu vou compartilhar um jogo que vai auxiliar o estudante a compreender e exercitar o cálculo do mínimo múltiplo comum ou, simplesmente, MMC, que é utilizado para resolver situações-problema e operar com frações heterogêneas (embora não seja necessário utilizar o MMC para somar e subtrair frações com denominadores diferentes), dentre outras aplicações.

O MMC de dois ou mais números naturais é o menor inteiro positivo que é múltiplo desses números simultaneamente e, para calculá-lo, sem fazer uso de qualquer algoritmo, basta encontrar o conjunto dos múltiplos de cada um dos números envolvidos e observar o menor múltiplo que é comum a eles.

Para iniciar a abordagem deste conteúdo nada melhor do que propor aos estudantes a resolução de situações-problema do cotidiano, tal como a que segue:

Dona Sara levou seu filho Paulinho ao médico pois ele estava com uma gripe muito forte. O médico examinou o menino e receitou dois remédios para serem administrados durante dois dias: um de 8 em 8 h e o outro de 6 e 6 h. Assim que retornou para casa às 8 h da manhã, Paulinho iniciou o tratamento ingerindo os dois remédios juntos.

• Quais os horários em que Paulinho tomará cada um dos remédios durante os dois dias do tratamento?
• Em qual(is) horário(s) Paulinho tomará os dois remédios juntos novamente?
• Se Paulinho tivesse iniciado o tratamento ao meio dia ingerindo os dois remédios, em qual(is) horário(s) ele tomaria os remédios juntos?

Para resolver o problema é muito importante que os alunos possam trocar ideias com os colegas, então a organização da turma em duplas ou trios é uma ótima ideia. Os grupos podem discutir, fazer anotações e criar estratégias para resolver o problema.

Depois que os grupos resolveram o problema é hora de cada um explicar ao grande grupo como pensou, de que forma resolveu a situação e que respostas encontrou. É importante observar que mais de um caminho pode solucionar o desafio e a socialização das estratégias cria um espaço de discussão e aprendizagem na sala de aula.

Uma das maneiras de resolver a primeira pergunta do problema é fazendo a listagem dos horários de administração de cada um dos remédios partindo do horário inicial de ingestão até o final do tratamento.

Remédio A: 8 h - 14 h - 20 h - 2 h - 8 h - 14 h - 20 h - 2 h - 8 h

Remédio B: 8 h - 16 h - 0 h - 8 h - 16 h - 0 h - 8 h

Observando os horários que são comuns a ambas as listagens percebe-se que a cada 24 horas os remédios são ingeridos juntos novamente e isso vai ocorrer sempre às 8 h da manhã. Essa é a resposta da segunda pergunta.

Se Paulinho tivesse iniciado o tratamento ao meio dia, os horários de administração dos remédios seriam os seguintes:

Remédio A: 12 h - 18 h - 0 h - 6 h - 12 h - 18 h - 0 h - 6 h - 12 h

Remédio B 12 h - 20 h - 4 h - 12 h - 20 h - 4 h - 12 h

e os dois remédios seriam tomados juntos ao meio dia dos outros dias de tratamento. Observa-se que, independentemente do horário inicial, a cada 24 horas os dois remédios são ingeridos juntos novamente. E porque isso ocorre?

A organização dos horários leva em consideração os múltiplos de 6 e de 8, tomados em relação às horas do dia. Veja o que acontece quando escrevemos os conjuntos dos múltiplos desses números:

M(6)={ 6, 12, 18, 24, 30, 36,...}

M(8)={8, 16, 24, 32, ...}

ou seja, pode-se observar que 24 é o menor múltiplo comum entre 6 e 8, logo MMC(6,8)=24 e é por isso que, a cada 24 horas, os dois remédios são ingeridos juntos.

Outros problemas similares e em diferentes contextos podem ser propostos para que os alunos reflitam sobre o mínimo múltiplo comum e assimilem este conceito.

Após as problematizações, que tal apresentar um jogo para descontrair a turma?

O jogo que segue vai ajudar o estudante a compreender e exercitar o cálculo do MMC sem o uso de qualquer algoritmo. Os alunos ficam em duplas e cada uma recebe uma tabela e uma canetão para quadro branco. Gosto de colocar a tabela dentro de um saquinho plástico transparente pois, após o jogo ser concluído, os estudantes limpam as anotações feitas com o canetão utilizando um pedaço de papel higiênico e a tabela fica prontinha para novas jogadas.

Decide-se no par ou ímpar quem começa a jogar e cada jogador deverá escolher dois números quaisquer posicionados na base do robô e calcular o MMC entre eles a partir da construção do conjunto dos múltiplos. Este jogador irá marcar, no corpo do robô, com um círculo ou X (como no jogo da velha) o MMC encontrado . Em seguida, o outro jogador fará o mesmo e assim prosseguirá a atividade. Será vencedor aquele que primeiro alinhar 4 números (na horizontal, vertical ou diagonal).

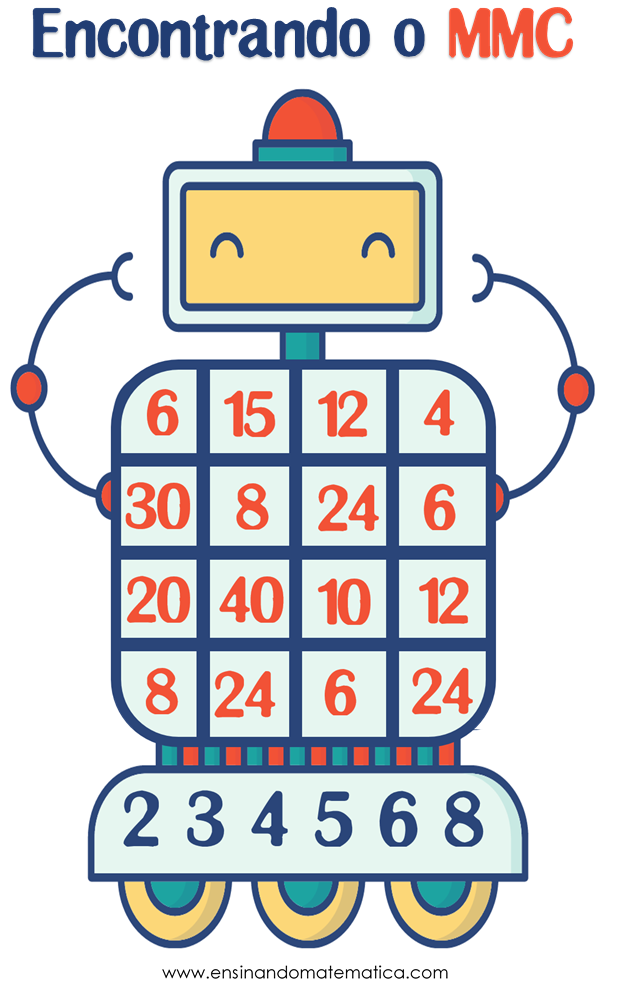
CLIQUE AQUI PARA FAZER DWONLOAD DA TABELA DO JOG0.

Após o jogo vamos problematizar algumas situações para que os estudantes reflitam um pouco mais sobre o MMC:

• Descubra todas as duplas de números que estão na base do robô que têm MMC igual a 6.
• Descubra todas as duplas de números que estão na base do robô que têm MMC igual a 12.
• Para qual(is) dupla(s) de números o MMC é 40?
• Por que o MMC entre 2 e 5 é o produto destes números (10) e o MMC entre 2 e 4 não é o produto de 2 e 4?
• Encontre cinco pares de números (na base do robô) cujo MMC é o produto entre eles.
• Encontre cinco pares de números (na base do robô) cujo MMC não é o produto entre eles.

Quando números maiores são envolvidos nas situações-problema é necessário apresentar aos alunos um algoritmo para o cálculo do MMC e aí é a técnica da decomposição simultânea em fatores primos será bastante útil.

Outros problemas muito interessantes envolvendo o mínimo múltiplo comum podem ser encontrados no caderno "O professor PDE e os desafios da Escola Paranaense" referenciada logo abaixo.

REFERÊNCIAS BIBLIOGRÁFICAS

CARVALHO, Donizetti Baltazar. Resolução de problemas: uma possibilidade para o ensino do mínimo múltiplo comum e do máximo divisor comum. O PROFESSOR PDE E OS DESAFIOS DA ESCOLA PARANAENSE. Volume II. Disponível em: . Acesso em 18 out. 2020.