Você, professor, têm facilidade em fazer cálculos mentais? Com certeza, sim! Nós, professores, pais, sabemos responder com rapidez quanto é 8 + 7, 5 + 6, 4 + 9, ... Aprendemos e memorizamos essas somas quando éramos crianças e sabê-las de cor facilita, em muito, a nossa vida! A maioria das crianças de hoje, lamentavelmente, não tem tanta agilidade mental quanto gostaríamos. O que fazer, na sala de aula, para desenvolver o pensamento matemático de nossos alunos e ajudá-los na aplicação das propriedades e memorização dos fatos básicos da adição?
![]() De acordo com o Pró Letramento: Matemática, fatos básicos são cálculos com números de um só algarismo que devem ser realizados mentalmente e sem o auxílio do algoritmo (conta armada). Então, 3 + 4 =7, 6 + 6 = 12 e 9 + 5 = 14, por exemplo, são alguns fatos básicos ou fundamentais da operação de adição. Quem é que nunca foi ao mercado com o dinheiro contado? Ah, nessas situações, por exemplo, precisamos fazer cálculos rápidos, enquanto colocamos as compras no cestinho, para chegar ao caixa e não termos problemas com o pagamento. O que a maioria faz é arredondar os valores e somar os números redondos para estimar o gasto total. Porém, para que essa tarefa seja bem sucedida, é preciso ter construído e memorizado os fatos básicos da adição. Todavia, de nada adianta a memorização sem a compreensão do processo aditivo. Quando memorização e compreensão estão articuladas, há uma potencialização da aprendizagem.
De acordo com o Pró Letramento: Matemática, fatos básicos são cálculos com números de um só algarismo que devem ser realizados mentalmente e sem o auxílio do algoritmo (conta armada). Então, 3 + 4 =7, 6 + 6 = 12 e 9 + 5 = 14, por exemplo, são alguns fatos básicos ou fundamentais da operação de adição. Quem é que nunca foi ao mercado com o dinheiro contado? Ah, nessas situações, por exemplo, precisamos fazer cálculos rápidos, enquanto colocamos as compras no cestinho, para chegar ao caixa e não termos problemas com o pagamento. O que a maioria faz é arredondar os valores e somar os números redondos para estimar o gasto total. Porém, para que essa tarefa seja bem sucedida, é preciso ter construído e memorizado os fatos básicos da adição. Todavia, de nada adianta a memorização sem a compreensão do processo aditivo. Quando memorização e compreensão estão articuladas, há uma potencialização da aprendizagem.
A criança deve ter oportunidade de vivenciar diferentes experiências concretas envolvendo o conceito de adição para que seja capaz de interiorizá-lo e, depois, aplicá-lo em situações diversas e na aprendizagem do algoritmo.
Seguem, abaixo, algumas ideias!
Comprando palitos
Comprando palitos é um jogo em que as crianças irão constituir coleções a partir do do sorteio de palitos de picolé de duas cores. Essa atividade solicita a comparação e quantificação de conjuntos para descobrir, em cada rodada, quem comprou mais palitos. O material necessário para cada grupo de 3 crianças é o seguinte: 40 palitos de picolé, sendo 20 vermelhos e 20 amarelos; duas bandejas; dois dados comuns, sendo um vermelho e outro amarelo; folha para anotação; lápis; lápis de cor; 5 tampinhas. Primeiramente, os palitos são organizados nas bandejas, sendo uma para cada cor. A primeira criança a jogar lança os dois dados e toma a quantidade de palitos de cada cor sorteada ( o dado amarelo sorteia palitos amarelos e o dado vermelho indica a quantidade de palitos vermelhos). Os próximos jogadores fazem o mesmo, cada um em sua vez. Após, cada jogador faz uma construção com seus palitos sobre a mesa e explica aos colegas o que ela representa. Todos observam as construções e verificam quem conseguiu mais palitos; este é o vencedor da rodada e recebe uma tampinha para marcar seu ponto. Em seguida, os jogadores preenchem um relatório, tal como o modelo abaixo:
![]()
O palitos são recolocados nas bandejas e nova rodada é iniciada. São feitas cinco rodadas e o vencedor do jogo é aquele que ganhou mais tampinhas.
Totalizando 5
Essa atividade, adaptada do jogo "Explorando todas as adições possíveis de uma única soma" (RANGEL), tem como objetivo encontrar todas as adições que tenham 5 como resultado. De acordo com a autora, para que a estrutura operatória da adição no campo de 0 a 10 se consolide é necessário propor diferentes jogos que explorem todas as possíveis adições de um determinado total. O material necessário é o seguinte: uma cartela (modelo) para cada dupla de crianças, 5 tampinhas e um dado comum em que o número seis esteja substituído pelo número zero.
![]()
Cada criança, na sua vez, joga o dado que diz quantas tampinhas viradas para baixo devem ser colocadas na cartela. Nos demais círculos devem ser colocadas tampinhas viradas para cima. Por exemplo, se cair 3 no dado a situação no concreto é a seguinte: ![]() E a criança registra a sentença matemática: 3 + 2 = 5. Assim, cada estudante jogará o dado e poderá registrar por desenho e por escrito a situação contemplada, até que todas as adições possíveis tenham sido encontrada. Caso uma jogada repita alguma situação já encontrada, joga-se novamente. Convém destacar que a situação 2 + 3 = 5 é diferente da anterior já que serão 2 tampinhas viradas para baixo e 3 para cima:
E a criança registra a sentença matemática: 3 + 2 = 5. Assim, cada estudante jogará o dado e poderá registrar por desenho e por escrito a situação contemplada, até que todas as adições possíveis tenham sido encontrada. Caso uma jogada repita alguma situação já encontrada, joga-se novamente. Convém destacar que a situação 2 + 3 = 5 é diferente da anterior já que serão 2 tampinhas viradas para baixo e 3 para cima:
![]()
No total são seis as possíveis frases aditivas:
0 + 5 = 5 1 + 4 = 5 2 + 3 = 5 3 + 2 = 5 4 + 1 = 5 5 + 0 = 5
Além de explorar a propriedade comutativa e elemento neutro da adição, essa atividade favorece o desenvolvimento da estrutura numérica do pensamento da criança porque a faz refletir sobre as diferentes maneiras de encontrar um mesmo total.
Para outros totais, pode-se adaptar o jogo utilizando uma roleta ao invés do dado.
Jogo Monstrinho das Somas
Clique aqui para fazer download da tabela do jogo Monstrinhos das Somas
Totalizando 7
A ideia da prática que descrevo a seguir veio de uma palestra que assisti com a professora Ana Cristina Rangel, há muitos anos atrás. Achei super interessante e, por isso, estou compartilhando aqui. Com o mesmo propósito da atividade anterior, "Totalizando 7" utiliza como material caixas de fósforos e feijões graúdos. A caixa tem que ter uma divisão central na parte interna (fósforos longos) e ser preparada conforme a imagem abaixo, em que foi feita uma abertura na divisória para a passagem dos feijões.
![]()
São colocados 7 feijões na caixa sendo que cada grupo de 3 crianças deve ter uma caixa para realizar a atividade. Cada criança, na sua vez, sacode a caixa de fósforos e, ao abri-la, encontrará diferentes quantidades de feijões nas duas partes da caixa. Então, o trio escreverá uma frase matemática aditiva associada à situação e a registrará também através de desenho. Por exemplo:
![]()
![]()
Depois é a vez do colega seguinte fazer o mesmo, ou seja, ele fecha a caixa e a sacode. Ao abri-la, encontrará os feijões distribuídos de maneira diferente entre as duas partes. Assim, novo desenho e frase matemática aditiva são produzidos. Combina-se que o grupo deverá encontrar todas as frases matemáticas possíveis com o total 7 e quando uma situação (frase) é repetida, a criança refaz o procedimento. A caixa vai passando de mão em mão até que o trio consiga encontrar as 8 frases aditivas possíveis:
0 + 7 = 7 1 + 6 = 7 2 + 5 = 7 3 + 4 = 7 4 + 3 = 7 5 + 2 = 7 6 + 1 = 7 7 + 0 = 7
Modificando-se a quantidade de feijões na caixa obtém-se as somas possíveis para outros totais.
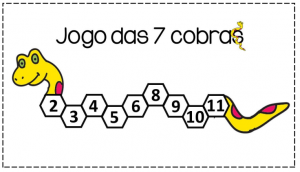
Jogo das sete cobras
Este jogo é conhecido, porém fiz algumas modificações nas regras para torná-lo mais dinâmico. Ele auxilia na fixação dos fatos fundamentais da adição e possibilita a exploração de probabilidades. Os alunos devem organizar-se em duplas, trios ou quartetos e cada grupinho receberá dois dados comuns em cores diferentes. Na face 6 de um dos dados será colada uma etiqueta com a imagem de uma estrela.
![]()
Cada estudante, de posse de uma folha de papel e lápis ou caneta, deverá escrever na folha os numerais que seguem abaixo:
![]()
Estabelece-se uma ordem para o jogo; o primeiro a jogar lança os dois dados e soma os números das faces. Ele deve riscar da sua listagem numérica o resultado da soma obtida e, caso o número seja 7, deve desenhar uma cobra. O jogador seguinte faz o mesmo e assim sucessivamente. Quando aparecer em um dos dados a estrela, o número do outro dado é ignorado e o jogador escolhe se deseja riscar um número qualquer da listagem ou desenhar uma cobra. Se a soma obtida já foi riscada, o competidor passa a vez. O jogo termina quando um dos jogadores tiver riscado todos os números ou desenhado 7 cobras. As duas possibilidades de vencer o jogo são as seguintes:
![]()
![]()
CLIQUE AQUI PARA FAZER O DOWNLOAD DA TABELA DO JOGO
Após o jogo, podem ser propostas atividades de pesquisa e discussão sobre os possíveis valores dos dados para os diferentes resultados. Assim, os alunos perceberão que há várias possibilidades para a ocorrência do número 7, quais sejam, 1+6=7, 6+1=7, 2+5=7, 5+2=7, 4+3=7, 3+4=7 e poucas possibilidades para a ocorrência, por exemplo, do número 3: 1+2=3 e 2+1=3. Dessa forma, as crianças dar-se-ão conta de que quanto mais possibilidades de ocorrência, maior a chance de um determinado resultado ser obtido. Os números com menor probabilidade de ocorrência são o 2 e o 11 pois, cada um, tem apenas uma única possibilidade de ocorrer (1+1=2 e 6 +5=11). O jogo das sete cobras pode ser proposto em diferentes momentos da aula e para diferentes faixas etárias e, de forma descontraída, permite a memorização de somas que tornarão ágil o pensamento matemático e auxiliarão nos cálculos mentais.
Somando 10
“Somando 10” é um jogo de tabuleiro quadriculado, em que os jogadores devem procurar obter a soma 10 adicionando quatro números (cartas) enfileirados na vertical, horizontal ou diagonal. O material necessário para cada grupo de 3 ou 4 alunos é o seguinte: tabuleiro quadriculado de 32 cm x 32 cm (modelo), cartinhas de 7 cm x 7 cm distribuídas da seguinte forma: numeral 1 (20 cartinhas), numeral 2 (20 cartinhas), numeral 3 (15 cartinhas), numeral 4 (10 cartinhas), numeral 5 (5 cartinhas), numeral 6 (2 cartinhas).
![]()
Inicialmente, as cartinhas são embaralhadas e cada jogador toma 3 para si; as demais ficam viradas para baixo em uma pilha. O tabuleiro é posicionado dentre os jogadores e cada um, na sua vez, deve colocar uma carta em uma quadrícula do mesmo. O jogador deve pescar uma carta do monte sempre que retirar uma de seu trio de cartas. O competidor que conseguir colocar a quarta cartinha que feche a soma 10 em uma linha, coluna ou diagonal, toma as quatro para si e marca um ponto. As cartas tomadas do tabuleiro não retornam ao jogo (são colocadas de lado).
![]()
Qualquer carta pode ser colocada em qualquer quadrícula do tabuleiro, mesmo que a soma da linha, coluna ou diagonal em que ela esteja seja diferente de 10. Porém o ponto é marcado pelo jogador que conseguir fechar a soma 10 a partir da colocação de sua cartinha em uma fileira que já possui outras três cartas.
![]()
No caso de não haver mais cartinhas para pescar, passa-se a vez. O jogo termina quando um dos competidores não dispuser de números para colocar no tabuleiro ou quando este estiver completo e nenhum quarteto de cartinhas possa ser retirado. É vencedor aquele que fizer mais pontos. Após o jogo, o professor pode solicitar à classe que escreva algumas frases matemáticas aditivas com quatro números que poderiam resultar em pontos no jogo. Por exemplo: 5+2+2+1=10 ou 3+3+3+1=10.
O quadro Valor de Lugar (QVL)
O Quadro Valor de Lugar, conforme o próprio nome já diz, é uma tabela na qual estão indicadas as casas ou ordens do nosso sistema de numeração, quais sejam, unidade, dezena, centena, etc. Este material é utilizado para reforçar a representação posicional dos números e é um excelente recurso para ser utilizado na ampliação do campo numérico e nas operações. O QVL poderá especificar, inicialmente, grupos de dez palitos e palitos soltos para, numa etapa seguinte, mostrar dezenas (D), unidades (U) e outras ordens.
![]()
Algoritmo da adição sem reagrupamento
Material: QVL, palitos de picolé, atilhos, material dourado
Para trabalhar concretamente adições com total menor que 100 sugere-se que o professor utilize palitos de picolé e atilhos já que este material possibilita uma melhor compreensão dos processos. Para números maiores que 100, o material dourado é o mais indicado.
As operações são realizadas com o material concreto e pelo algoritmo. Quando do uso de palitos e atilhos, as tiras indicadoras de cada coluna do QVL podem, num primeiro momento, apresentar as imagem dos grupos de dez (dezena) e do palito solto (unidade). Seguem alguns exemplos:
![]()
Algoritmo da adição com reagrupamento
Material: QVL, palitos de picolé, atilhos, material dourado O reagrupamento na operação de adição, chamado popularmente de “reserva”, ocorre quando mais do que 9 elementos ficam em uma determinada casa em consequência da adição. Como isso não pode acontecer, devido às regras do sistema de numeração decimal, os elementos são reagrupados para ocuparem outras casas. Na introdução da operação de adição com reagrupamento são utilizados palitos de picolé e atilhos e, mais tarde, o material dourado. Com os palitos e atilhos o reagrupamento é bastante concreto e compreensível para a criança devido ao fato de que dez palitos na casa das unidades, por exemplo, são amarrados para formar um "amarradinho" que, por sua vez, deve ser transferido para a casa das dezenas. Seguem alguns exemplos:
![]()
Referências Bibliográficas
MINISTÉRIO DA EDUCAÇÃO. Secretaria de Educação Básica. Pró-Letramento: programa de formação continuada de professores dos anos/séries iniciais do Ensino Fundamental: Matemática. Fascículo 1: Números Naturais. Brasília, 2007. Disponível em: Acesso em 04 jan. 2017.
RANGEL, Ana Cristina S. Educação matemática e a construção do número pela criança. Porto Alegre: Artes Médicas, 1992





















Ivanise Meyer
10/06/2018 09:20
http://www.baudeideiasdaivanise.blogspot.com
Roselice
10/06/2018 17:40