
Calendário interativo para os anos iniciais
01/10/2025
Aprenda a construir e explorar o calendário com a turma de forma atrativa e inteligente, desenvolvendo noções de medidas de tempo e interpretação de dados.

Ontem mesmo estava trabalhando com uma turma de Pré-Cálculo, disciplina da grade curricular de Cursos de Engenharia e, ao resolver um exercício no quadro, perguntava aos alunos: "2/3 x 4 quanto dá?" ... Nenhuma resposta! "Como faço 1/2 -3 ?" ... Silêncio na sala de aula! ????????? !!!!!!!! Eles não sabiam responder. São graduandos em início de curso. Terminaram o Ensino Médio a pouco tempo. Que lástima!
Sei, há tempos, que os estudantes chegam no ensino superior com muita dificuldade em entender e operar com frações. Sei, também, que os professores de matemática do ensino fundamental ensinaram frações para eles. Certamente há um problema no ensino das frações já que são poucos os alunos que realmente compreendem esse assunto.
Acredito veementemente que o problema está no ensino baseado em quadro, livro e giz e desvinculado da manipulação de materiais adequados e de atividades ricas de significado. Vou então sugerir uma sequência de atividades práticas e com material concreto, testadas e comprovadas, para ensinar frações . Os materiais são bastante simples e fáceis de construir ou conseguir. Vamos lá!
Esta atividade pretende introduzir as frações a partir situações partitivas. A turma é dividida em grupos de quatro e o professor propõe a resolução de algumas situações problema, tais como as que seguem, solicitando que sejam resolvidas através de desenho e frase matemática de divisão:
Com certeza, é possível fazer essa divisão. Cada criança receberá 4 lápis e não sobrará lápis.
Nesta divisão cada vaso recebeu 3 flores e houve uma sobra de duas flores. As flores restantes não puderam ser repartidas entre os quatro vasos.
Sim, dá para realizar a divisão. Ocorreu a sobra de uma pizza que foi repartida entre as três pessoas e o resultado da divisão é um número não inteiro. Como as crianças ainda não conhecem frações, elas podem escrever por extenso a porção de pizza que coube a cada pessoa. É interessante comparar os três exemplos: no primeiro não sobrou resto e o resultado da divisão é um número inteiro; no segundo, o resultado é um número inteiro mas sobrou resto e este não pôde ser dividido; no terceiro caso sobrou resto e ele foi repartido resultando numa divisão com resultado não inteiro. Após a discussão com a turma de outras situações similares surgirá a necessidade de introduzir números que representam frações do inteiro.
Com a turma ainda organizada em grupos, vamos distribuir muitas folhas de papel aos grupos. Sugiro utilizar folhas de rascunhos. Cada aluno toma algumas folhas para si e faz o que é solicitado: a) Dobrar o papel ao meio e pintar (ou hachurar) uma parte. Abrir o papel e observar em quantas partes a folha ficou dividida e quantas partes foram pintadas. Como foi pintada 1 das 2 partes em que a folha foi dividida, a parte pintada corresponde a 1/2 ou metade da folha. Escrever 1/2 sobre a parte pintada (o professor registra no quadro a fração numericamente e por extenso).
b) Tomar outra folha de papel e dobrar ao meio. Dobrar a folha ao meio novamente e pintar uma parte. Abrir a folha e verificar que foi pintada 1 das 4 partes. Registrar 1/4 sobre a parte pintada (registro no quadro feito pelo professor).
c) Tomar a folha de papel e dobrá-la como em (b). Dobrar a folha ao meio novamente e pintar uma parte. Abrir a folha e verificar que foi pintada 1 de 8 partes. Escrever 1/8 sobre a parte pintada (registro no quadro feito pelo professor).
d) Tomar uma folha de papel e fazer um rolinho dividindo-a em três partes: 
Fonte: WikiHow
Pintar 1 das 3 partes em que a folha foi dividida e registrar sobre a parte pintada a fração 1/3 (registro no quadro feito pelo professor).
e) Dobrar a folha como em (d) e, depois, dobrá-la ao meio. Pintar uma das partes e abrir a folha observando que 1 das 6 partes foi pintada. Registrar sobre a parte pintada a fração 1/6 (registro no quadro feito pelo professor).
f) Dobrar a folha como em (d) fazendo um rolinho. Depois, dobrá-la em 3 partes novamente. Pintar uma das partes e abrir a folha. Escrever sobre a parte pintada 1/9 visto que foi pintada 1 das 9 partes em que a folha foi dividida (registro no quadro feito pelo professor).
Depois de feitas as dobraduras indicadas acima, o professor solicita que os alunos organizem as frações em ordem decrescente, a partir da observação e comparação das partes pintadas em cada uma das folhas. Os estudantes facilmente conseguirão escrever que:
As frações são escritas através de dois números, quais sejam, o numerador e o denominador. O numerador numera, isto é, diz quantas partes foram tomadas ou pintadas. o denominador denomina, dá nome à fração.
Costumo comparar as frações com famílias. Cada membro da família tem nome e sobrenome. O sobrenome dá características à família, tais como: são descendentes de italianos, são pessoas altas e de cabelos escuros, etc. Neste momento, costumo perguntar às crianças seus sobrenomes e os aspectos gerais de suas famílias.
Assim, a família dos meios, por exemplo, é formada por partes grandes e de cor vermelha (tal como pintado na imagem da dobradura) e a família dos nonos tem na sua formação partes pequenas e de cor azul.
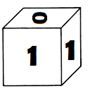
Para as atividades que seguem será necessário que cada criança confeccione discos fracionários a partir de um modelo fornecido. Serão utilizados, para cada aluno, um inteiro, 2/2, 4/4, 8/8 e, para cada dupla, um dado com os numerais: 0, 0, 1, 1, 1, 1. A construção do material pode ser proposta como tarefa extraclasse; os discos devem ser recortados e pintados em cores previamente combinadas. Sugiro discos de raio 10 e as cores branca para o inteiro, vermelha para os meios, roxa para os quartos e marrom para os oitavos.
As crianças compõem duplas e, primeiramente, deve ocorrer a exploração do material e os recobrimentos das peças. Essa parte da atividade é muito importante, porque os alunos verificarão as equivalências entre as frações e descobrirão, por exemplo, que 2/4 cobrem 1/2, 4/8 cobrem 1/2, 2/2 cobrem o inteiro, 6/8 cobrem 3/4, e assim por diante.
Depois da exploração, o professor pode fazer questionamentos aos grupos, tais como:
As duplas terão como desafio produzir receitas de pizzas envolvendo os discos fracionários meios, quartos e oitavos. Cada pizza deverá ser formada por, pelo menos, dois sabores (cores). A turma poderá relacionar as cores aos sabores de pizza. Assim, por exemplo, cada meio pode ser uma porção de pizza de calabresa, cada quarto representa uma fração de pizza de berinjela e cada oitavo é uma fatia de pizza de chocolate. As receitas serão escritas através de frases aditivas, tais como mostra a figura abaixo:  As crianças gostam muito de realizar esta atividade e as frases aditivas surgem espontaneamente para registrar as "receitas". Quero salientar que não é intuito explicar, neste momento, a adição de frações heterogêneas.
As crianças gostam muito de realizar esta atividade e as frases aditivas surgem espontaneamente para registrar as "receitas". Quero salientar que não é intuito explicar, neste momento, a adição de frações heterogêneas.
Em duplas e de posse do dado, cada jogador fica com o seu material (inteiro, meios, quartos e oitavos). Há três fases para o jogo. Na primeira, utilizam-se apenas as peças marrons (oitavos) e o inteiro, além do dado. Cada jogador posiciona o inteiro à sua frente e, na sua vez, lança o dado que determina quantas peças marrons devem ser colocadas sobre o inteiro. Vence o jogo aquele que primeiro completar seu inteiro com peças marrons (oitavos).
Para a segunda fase do jogo são utilizados o inteiro, os oitavos (peças marrons) e os quartos (peças roxas). Cada jogador posiciona o inteiro à sua frente e, na sua vez, lança o dado que determina quantas peças marrons devem ser colocadas sobre o inteiro. Cada duas peças marrons podem ser trocadas por uma roxa e, se o jogador fizer a troca, terá direito de jogar novamente. Vence o jogo aquele que primeiro completar seu inteiro.
Na terceira fase são utilizadas todas as peças. Como anteriormente, cada jogador posiciona o inteiro à sua frente e, na sua vez, lança o dado que determina quantas peças marrons devem ser colocadas sobre o inteiro. Cada duas peças marrons podem ser trocadas por uma roxa e cada duas peças roxas podem ser trocadas por uma vermelha. Se o jogador fizer esta última troca, terá direito de jogar novamente. Vence o jogo aquele que primeiro completar seu inteiro.
É importante salientar que o aluno estabelece uma relação entre a fração e a cor utilizada na construção dos discos fracionários. Assim, aos poucos, ele vai associando cor-fração e criando uma imagem mental para essas frações. O mesmo jogo pode ser proposto para outras famílias de frações, tais como, inteiro - quintos - décimos ou inteiro - terços - sextos ou, ainda, inteiro – terços – sextos - nonos. O grande mérito dessa atividade é formar grupos (famílias) de frações em que é possível estabelecer correspondências. Assim, aos poucos, os estudantes apropriam-se dos conhecimentos adquiridos sobre os conceitos e não os esquecem nunca mais.
O objetivo da atividade descrita a seguir é trabalhar o conceito de fração sob a ideia de divisão a partir de um inteiro discreto, ou seja, constituído por um conjunto de objetos que podem ser fichas ou tampinhas. Para continuar na brincadeira das pizzas, poderemos supor que sejam rodelas de calabresa ou cubinhos de queijo. Que tal? Sendo assim, os alunos continuam em duplas e ficam com os mesmos discos fracionários já mencionados (inteiro, meios, quartos e oitavos) e, ainda, em torno de 30 fichas ou tampinhas. O professor solicita que cada estudante forme o inteiro com os quartos e distribua igualmente 20 fichas sobre as partes. Os alunos descobrirão que 1/4 de 20 dá 5, que 2/4 de 20 dá 10 e assim por diante.
E quanto é 3/8 de 16?
Para responder a essa questão os alunos tomam os oitavos e 16 tampinhas e, em seguida, distribuem igualmente as tampinhas sobre os oitavos.
Depois de garantida a compreensão do processo de divisão envolvida no conceito de fração de forma concreta, é possível propor atividades similares sem os discos. Para isso, os alunos deverão pensar quais os cálculos são necessários para encontrar as frações de um conjunto de objetos.
Professor, há muito mais a sugerir no ensino de frações. Não deixe de ler Mais sobre frações - parte 2.
Teste essas ideias e me envie os comentários!
COMO dobrar um papel em terços. Disponível em: Acesso em 24 mar. 2017.
MARANHÃO, Cristina S. de A.; IMENES, Luiz Márcio P. Jogos com frações. Revista do Ensino de Ciências, n. 14, p. 47-51, set. 1985
01/10/2025
Aprenda a construir e explorar o calendário com a turma de forma atrativa e inteligente, desenvolvendo noções de medidas de tempo e interpretação de dados.
14/05/2024
Calcular medidas de posição e dispersão a partir de dados coletados na própria turma e que são oriundos de atividades práticas e diferenciadas certamente será muito mais significativo para os estudantes. Conheça propostas inéditas para ensinar estatística nos anos finais do EF e no ensino médio.
12/02/2024
Para auxiliar o professor no preparo de aulas envolvendo o sistema monetário, elaborei um e-book que contempla 18 jogos e atividades dinâmicas e atrativas, direcionados aos estudantes do 1º ao 5º anos do ensino fundamental.
Este site usa cookies para proporcionar uma melhor experiência para você. Ao prosseguir, você concorda com nossas Políticas de Cookies e de Privacidade. Saiba mais


Maria Cristina
18/05/2018 20:13