Mais sobre frações -parte 2

No artigo Entre pizzas e frações descrevi algumas atividades bem interessantes para introduzir frações a partir de diferentes estratégias e materiais. Neste artigo vou continuar dando sugestões de como avançar no estudo de frações utilizando materiais concretos e ideias bem legais. Vamos lá?

Jogo do Mico

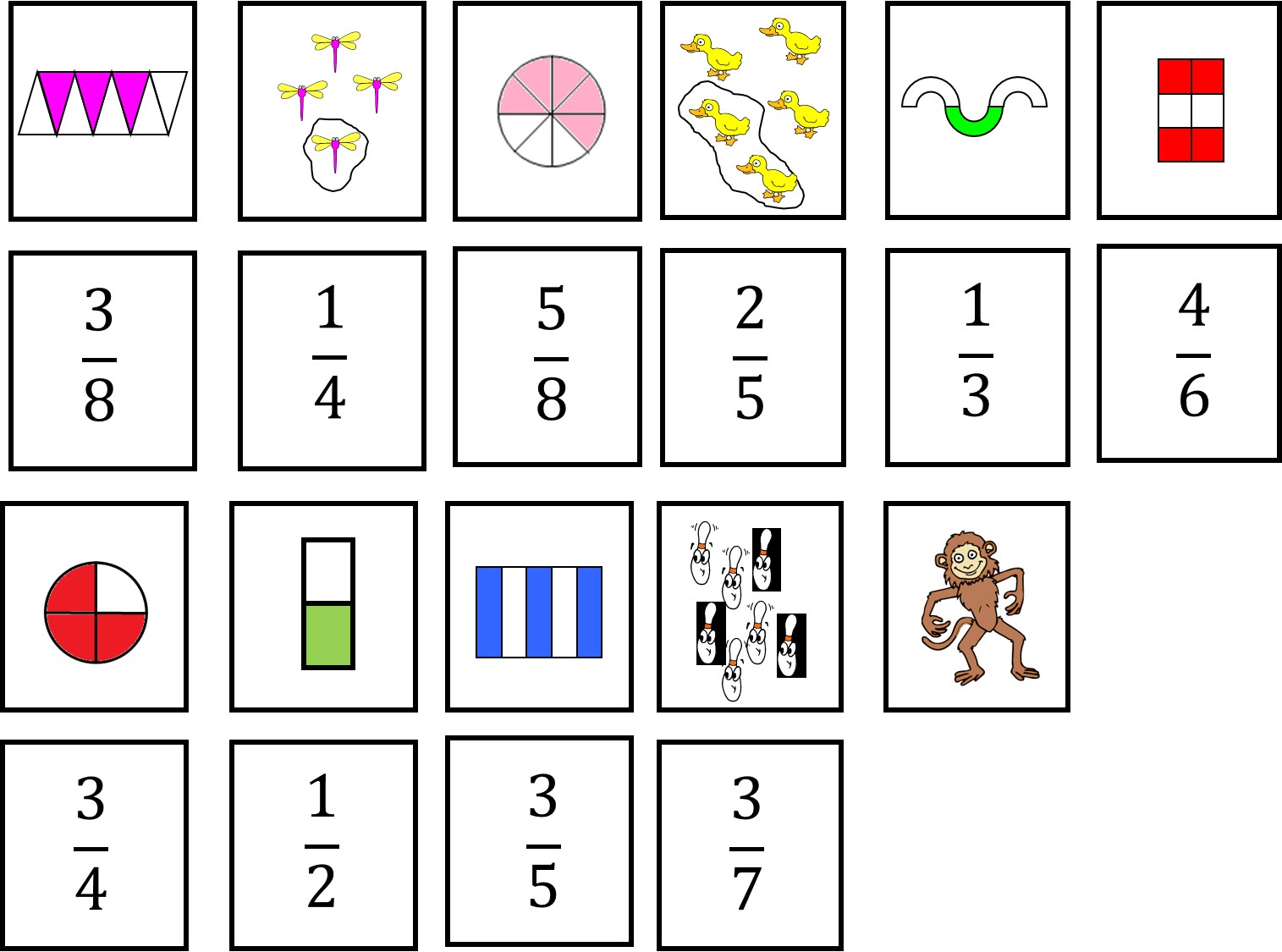
Para fazer correspondências entre fração e sua representação através de desenho uma boa estratégia é confeccionar o jogo do Mico. Como todos sabem, neste jogo é preciso elaborar cartas com pares, no caso fração-desenho, e deixar uma carta sem par que será o Mico. Segue, abaixo, uma sugestão de cartinhas: Clique aqui para obter uma cópia das cartinhas.

Joga-se em grupos de quatro e todas as cartas são distribuídas igualmente entre os jogadores. Inicialmente, cada componente do grupo separa os pares possíveis (figura-notação correspondente) e deixa-os sobre a mesa.

O primeiro jogador deverá retirar uma carta do seguinte. Se formar um par, coloca-o sobre a mesa e joga outra vez, até tirar uma carta que não tenha par. Em seguida, passa a vez para o próximo jogador e assim prossegue o jogo. Perde o jogo quem ficar com o mico na mão.

Menor, maior ou igual ao inteiro x número misto

Para esta atividade é preciso que cada aluno construa um conjunto de discos fracionários. Sugiro utilizar cartolina ou papel cartão e construir discos de raio 8 cm ou 10 cm a partir de um modelo tal como o que segue abaixo. É interessante, também, combinar com a turma previamente as cores em que os discos deverão ser pintados.

Clique aqui para obter o molde dos discos fracionários.

Após a construção dos discos e da exploração dos mesmos, em duplas, os estudantes descobrem se as frações dadas são menores que o inteiro, iguais ao inteiro ou maiores que o inteiro a partir da manipulação do material. Durante as descobertas o número misto surge de forma espontânea.

Por exemplo, sejam as frações 7/3, 6/2 e 3/4:

Aproveitamos, nesta atividade, para falar também fazer transformações de número misto em fração imprópria e vice-versa. Por exemplo:

a) Quais os números mistos representados pelas frações 5/4 e 9/2?

b) Quais as frações impróprias correspondentes aos números mistos que seguem abaixo?

Equivalências com dobraduras

Fica muito fácil encontrar frações equivalentes com dobraduras, tal como explico em seguida. Basta, para isso, distribuir para a turma folhas (de rascunho, de preferência) e lápis de cor ou canetinhas. Para encontrar frações equivalentes a 1/2  deve-se: a) Dobrar uma folha ao meio e pintar uma das partes. Abrir a folha e anotar no caderno a fração representada: 1/2. b) Deixar a mesma folha dobrada como em (a) e dobrá-la ao meio novamente. Abrir a folha e anotar no caderno a fração pintada: 2/4. c) Deixar a mesma folha dobrada como em (b) e, depois, dobrá-la ao meio novamente. Abrir a folha e anotar a fração representada: 4/8

O grande barato dessa atividade é o fato de que a pintura na folha é feita apenas na representação da primeira fração 1/2. Depois, são feitas outras dobras na folha e a parte pintada continua a mesma. Surgem, então, as frações 2/4 e 4/8.

d) Tomar outra folha avulsa, fazer um rolinho para dobrá-la em três partes. Pintar uma das partes. Abrir a folha e anotar a fração representada: 1/3.

e) Manter a folha como em (d) e, depois, dobrar ao meio. Abrir a folha e anotar a fração representada: 2/6.

f) Manter a folha como em (e) e, depois, dobrar ao meio novamente. Abrir a folha e anotar a fração representada: 3/9.

g) Tomar outra folha avulsa, fazer um rolinho e dobrá-la em três partes. Pintar uma das partes, abrir a folha e anotar a fração representada: 1/3.

h) Tomar a mesma folha dobrada como em (g) e dobrá-la, novamente, em três partes. Abrir a folha e anotar a fração representada.

Utilizando outras dobraduras, é possível encontrar mais equivalências. A partir da análise das frações equivalentes a uma dada fração, as crianças facilmente compreenderão que frações equivalentes são aquelas que representam a mesma porção do inteiro e, para encontrá-las, basta multiplicar ou dividir o numerador e o denominador por um mesmo número.

É muito simples: basta dobrar, observar e concluir a regra: para encontrar frações equivalentes a uma determinada fração basta multiplicar ou dividir o numerador e o denominador por um mesmo número.

Comparação de frações

Qual é a maior fração? Para responder a essa pergunta podemos realizar uma atividade em que os alunos descobrem regras a partir da comparação de frações com iguais denominadores, iguais numeradores ou, até mesmo, frações com numeradores e denominadores diferentes. A tabela fracionada, que apresento na imagem abaixo, vai ajudar nesta tarefa. Sugiro entregar uma tabela fracionada para cada aluno e solicitar a pintura das frações conforme as cores utilizadas nos discos fracionários.

Compare as frações a partir da observação da tabela fracionada. CASO 1: Frações com iguais numeradores

Todas as frações que estão sendo comparadas possuem igual numerador, então, qual é a maior fração? Aquela que tem o menor denominador porque as partes são maiores. Consequentemente, uma regra que poderia ser criada é:

quando duas frações tem igual numerador a maior fração é aquela que possuir o menor denominador

CASO 2: Frações com iguais denominadores

As frações do Caso 2 possuem, duas a duas, o mesmo denominador. Sendo assim, a maior fração é aquele que tem o maior numerador. Então:

quando duas frações possuem o mesmo denominador, a maior fração é aquela que tem o maior numerador

Caso 3: Frações com diferentes numeradores e denominadores Para comparar as frações deve-se transformar uma ou ambas as frações por meio de equivalência:

Quando duas frações possuem diferentes numeradores e denominadores deve-se transformá-las por equivalência e utilizar as regras estabelecidas nos casos anteriores.

No artigo Operações com frações - parte 3  abordo as operações com frações. Confira!!!