Professor, vamos partir do princípio que as tabuadas já foram construídas e que os alunos estão resolvendo situações-problema que envolvem as diferentes ideias da multiplicação. Queremos, agora, ensinar a operação de multiplicação com significado! Para tanto, vamos nos munir de alguns materiais, tais como: palitos de picolé, atilhos (elásticos de dinheiro), material dourado, QVL (quadro valor do lugar), folhas quadriculadas e lápis de cor.
A multiplicação por um número
Como ensinar a multiplicação por um número? Seja, por exemplo, a operação 3 x 12. Uma estratégia que recomendo é utilizar o QVL e os palitos de picolé a partir da ideia de adição de parcelas iguais da multiplicação.
![]()
Para resolver o cálculo é necessário tomar 12, três vezes. Como 12 é formado por uma dezena (um grupo de 10 palitos de picolé amarrados) e 2 unidades (2 palitos soltos), coloca-se no QVL três vezes essa quantidade de palitos. Somam-se as unidades e as dezenas e o resultado são 36 unidades.
Repetindo esse procedimento para outros casos como, por exemplo, 4 x 11, 2 x 14, etc. o professor pode conduzir ao algoritmo tradicional da multiplicação por um número, sem reserva. Nas operações com reserva, procede-se da mesma forma. Vamos analisar a operação 2 x 26.
![]()
A quantidade 26, formada por duas dezenas e 6 unidades, é repetida duas vezes no QVL. Ao adicionar as unidades, verifica-se que há 12 e, por isso, dez unidades devem ser amarradas para formar uma dezena e essa dezena é colocada na casa correspondente. Assim sendo, sobram 2 unidades na casa das unidades e 5 dezenas na casa das dezenas. O resultado são 52 unidades. O mesmo pode ser feito para as operações 4 x 23, 5 x 16, 6 x 13, etc. E, mais uma vez, fica fácil para o professor justificar as etapas do algoritmo da multiplicação por um número quando há reserva. Para operar com números maiores que 100, é mais indicado o uso do material dourado sendo que os procedimentos no QVL são semelhantes aos explicados com palitos de picolé e atilhos.
É importante destacar que, se a adição foi bem construída com os alunos, o algoritmo da multiplicação por um número será de fácil compreensão pelas crianças.
Multiplicação no papel quadriculado
Vamos, agora, utilizar desenho e pintura no papel quadriculado para fazer multiplicações por um número. Seja, por exemplo, o produto 4 x 13 e se deseja determinar o resultado do mesmo a partir da contagem da quantidade de quadradinhos cercada em um retângulo de 4 linhas e 13 colunas ou 4 colunas e 13 linhas.
Para facilitar a contagem de quadradinhos, a proposta agora é determinar esse produto subdividindo o 13 em uma soma, que pode ser, 7 + 6 ou 8 + 5 ou ... ou 10 + 3. Cada parte subdividida deve ser pintada de uma determinada cor.
Assim: ![]() Para obter a quantidade de quadradinhos cercada em cada retângulo basta fazer os cálculos 4 x 10=40 e 4 x 3=12 e adicionar os resultados. Então, 4 x 13 = 52. Outros exercícios similares podem ser propostos aos alunos e o que ser quer é que eles desmembrem o número composto em dezenas e unidades pois, desta forma, será mais fácil determinar o resultado final. Vejamos como ficam os produtos 8 x 15 e 6 x 14.
Para obter a quantidade de quadradinhos cercada em cada retângulo basta fazer os cálculos 4 x 10=40 e 4 x 3=12 e adicionar os resultados. Então, 4 x 13 = 52. Outros exercícios similares podem ser propostos aos alunos e o que ser quer é que eles desmembrem o número composto em dezenas e unidades pois, desta forma, será mais fácil determinar o resultado final. Vejamos como ficam os produtos 8 x 15 e 6 x 14.
![]()
![]()
Com muita facilidade, os alunos estão utilizando intuitivamente a propriedade distributiva da multiplicação em relação à adição. A compreensão desta propriedade é de fundamental importância para o entendimento dos algoritmos da multiplicação, especialmente da multiplicação por dois ou mais números.
Nosso próximo passo é operar com produtos do tipo 12 x 14 e, para tal, é preciso desmembrar o 12 em 10 + 2 e o 14 em 10 + 4. O resultado é um retângulo subdividido em 4 partes e cada parte deve ser pintada de uma cor diferente das demais. ![]()
Observamos que o resultado da operação 12 x 14 é obtido através de quatro produtos: 10 x 10 = 100, 10 x 4 = 40, 2 x 10 = 20 e 2 x 4 = 8 e 100+40+20+8=168, ou seja, 12 x 14 = 168. É muito interessante notar como se pode determinar de maneira fácil o produto 12 x 14 com este procedimento!
Assim, mais uma vez, se está utilizando de uma forma muito simples e de fácil compreensão a propriedade distributiva da multiplicação em relação à adição.
Mas, onde queremos chegar com isso? Na justificativa dos passos do algoritmo da multiplicação. Observe:
![]()
![]()
![]()
Ou seja, o algoritmo tradicional da multiplicação é construído a partir da aplicação da propriedade distributiva da multiplicação em relação à adição.
Com o entendimento desta propriedade, mesmo que de forma intuitiva, tal como feito nas atividades com o papel quadriculado, é fácil justificar para a turma porque se coloca um zero na casa das unidades (abaixo do 8 na conta acima). Repare que este zero forma o número 140, que é resultado do produto 10x14.
Muitos professores orientam os estudantes a deixarem uma casa vazia no lugar das unidades ou a colocarem o sinal "=" ou de "+". O correto é colocar o zero visto que, nesta posição, sempre haverá um número terminado em zero, que será o resultado do produto de um número redondo (10, 20, 30 ,...) por outro qualquer. Qualquer tentativa de explicar esse lugar vazio por meio de artifícios é pura invenção!!!


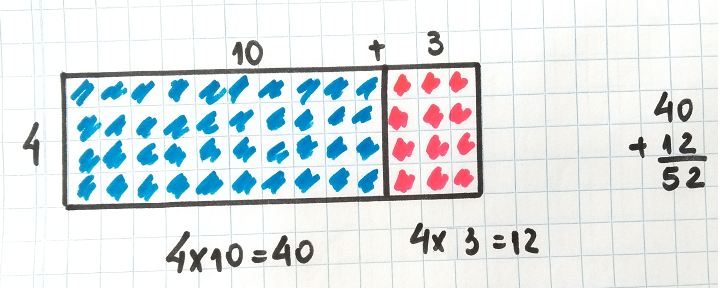 Para obter a quantidade de quadradinhos cercada em cada retângulo basta fazer os cálculos 4 x 10=40 e 4 x 3=12 e adicionar os resultados. Então, 4 x 13 = 52. Outros exercícios similares podem ser propostos aos alunos e o que ser quer é que eles desmembrem o número composto em dezenas e unidades pois, desta forma, será mais fácil determinar o resultado final. Vejamos como ficam os produtos 8 x 15 e 6 x 14.
Para obter a quantidade de quadradinhos cercada em cada retângulo basta fazer os cálculos 4 x 10=40 e 4 x 3=12 e adicionar os resultados. Então, 4 x 13 = 52. Outros exercícios similares podem ser propostos aos alunos e o que ser quer é que eles desmembrem o número composto em dezenas e unidades pois, desta forma, será mais fácil determinar o resultado final. Vejamos como ficam os produtos 8 x 15 e 6 x 14.

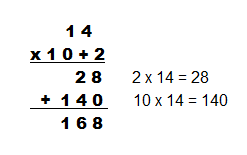
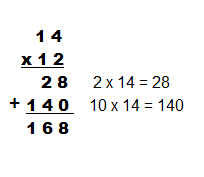




Roany Ribeiro
07/02/2018 22:00
http://operação%20de%20divisão